About Arithmetic Circuits
Arithmetic circuits consist of a collection of wires and gates, where the wires hold elements of a finite field and each gate computes either finite field addition or finite field multiplication. In contrast, in an electronic circuit, the wires either contain electrical signal or they don't, and each gate may compute a variety of logical operations.
Arithmetic circuits are central to zero-knowledge proof techniques: SNARKs and STARKs prove integrity of an execution of an arithmetic circuit.
Arithmetic Circuits as Polynomials
Because arithmetic circuits consist only of addition and multiplication, the circuit can be translated into a polynomial. In other words, the output(s) of the circuit can be expressed as a multi-variate polynomial, where
- is the number of inputs to the polynomial, and
- the degree of is bounded by the number of multiplications in the circuit.
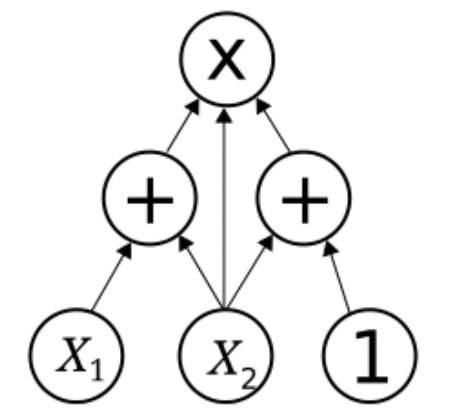
The circuit pictured above can be written as . This simple example is drawn from Wikipedia.
Two Approaches to Building with ZK
- Option 1: Build app-specific arithmetic circuits
- Option 2: Build on top of a zero-knowledge virtual machine, which receives a binary file as an input and outputs a proof of execution.
At RISC Zero, we adopt the latter approach: we've written a RISC-V circuit, which emulates rv32im. The rv32im circuit receives a RISC-V binary and some user specified input, and generates an execution trace.
If the execution trace is valid, the Prover generates a receipt that can be verified by a skeptical third party.
RISC Zero's Circuits
In addition to the rv32im circuit, we have built:
- an accelerator circuit for SHA-256
- a recursion circuit, which receives two receipts and produces a single recursion receipt.
Additional Resources
- Wikipedia page on arithmetic circuit complexity
- From programs to arithmetic circuits: YouTube video from David Wong